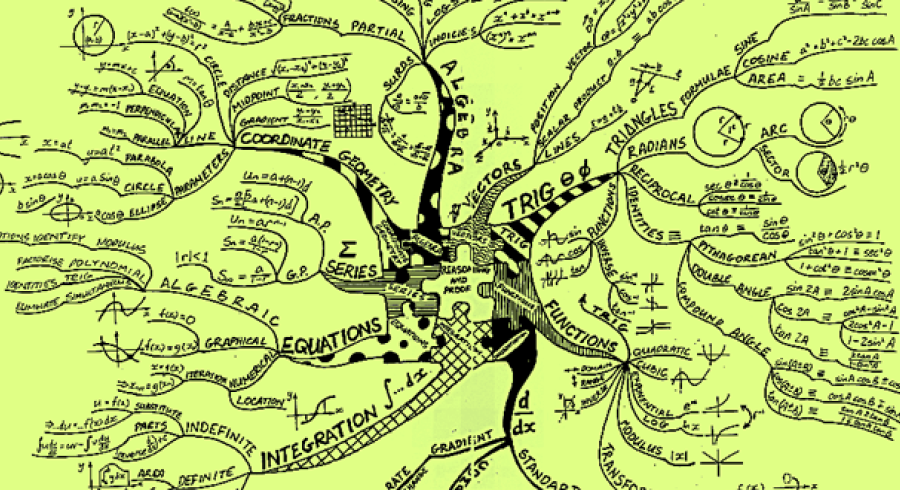
Quiero contarles que hay algo en lo que pienso con mucha frecuencia, y que discuto con otros compañeros en ocasiones: el problema entre la mayoría de la comunidad estudiantil y la Matemática, radica en que se pretende verla como algo arcano, lleno de misterio, casi de brujería. Por supuesto, ante semejante panorama, los sentimientos más comunes son de repulsión, aversión, hasta llegar a un miedo indescriptible. Incluso, para más de uno debe ser difícil visualizar y entender un mapa mental que muestre algunas ramas de la Matemática, como el siguiente:
Sin embargo, como alguna vez mencionó el matemático Douglas R. Hofstadter en su libro Gödel, Escher, Bach - An Eternal Golden Braid, su obra (que es en sí un estudio de la Matemática) trata enteramente sobre traducción:
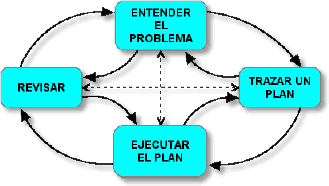 Esto aplica también en los procesos de solución de problemas, ya que no hay distinción entre los problemas matemáticos y los problemas no matemáticos, porque a fín de cuentas son problemas. La estrategia creada por el matemático húngaro George Pólya para la solución de problemas, si bien se ve, no muestra elemento alguno que no sea de aplicación general en todo contexto. La diferencia radica en el tipo de código que empleamos para la expresión de ese problema (según la información disponible) y, por consiguiente, para su solución y revisión.
Esto aplica también en los procesos de solución de problemas, ya que no hay distinción entre los problemas matemáticos y los problemas no matemáticos, porque a fín de cuentas son problemas. La estrategia creada por el matemático húngaro George Pólya para la solución de problemas, si bien se ve, no muestra elemento alguno que no sea de aplicación general en todo contexto. La diferencia radica en el tipo de código que empleamos para la expresión de ese problema (según la información disponible) y, por consiguiente, para su solución y revisión.
Considerando entonces que el pensamiento matemático es el pensamiento para explicar lo que observamos, y que el lenguaje matemático se comporta exactamente como nuestra lengua, pero empleando otros sistemas simbólicos, es posible decir dos cosas:
Algo al respecto escribimos mi compañero Sergio Gallo y yo, tratando de mostrar que, a partir de la concepción de la Matemática y la Música como lenguajes, es posible establecer una relación entre estos saberes y los métodos creados para la enseñanza de una segunda lengua. El texto está disponible en mi entrada de LinkedIn Pulse, Possibilities of Linguistic Teaching Methods on Musical and Mathematical Languages Learning: reflections about our practice.
En suma, el razonamiento matemático es el razonamiento en sí, pero empleando como forma de expresión un lenguaje rico en símbolos que dan forma a objetos, situaciones, momentos, fenómenos naturales, ¡incluso adivinanzas! (¿o acaso qué crees que significa "encriptar"?). No por nada se considera a la Matemática el Lenguaje Universal. Viéndolo así, ¿será que en la famosa Torre de Babel se hablaba en Matemático?
Hasta luego.
Sin embargo, como alguna vez mencionó el matemático Douglas R. Hofstadter en su libro Gödel, Escher, Bach - An Eternal Golden Braid, su obra (que es en sí un estudio de la Matemática) trata enteramente sobre traducción:
"GEB trata acerca de significado y símbolos, códigos e isomorfismos, conexiones y analogías; en breve, acerca de correspondencias, exactas e inexactas, entre diferentes sistemas en todos los niveles imaginables. Ésta es ciertamente la esencia de la traducción"Este pequeño cambio en nuestro punto de vista, permite tener en cuenta nuestra capacidad para la adquisición de una nueva lengua, para desdibujar ese terrible paradigma del pensamiento matemático como el más difícil, aburrido y peligroso de todos los saberes (peligroso en el sentido de que las pretensiones de pasar un curso de Matemática son utópicas). Es sólo cuestión de considerar que la Matemática tiene un lenguaje, un sistema de símbolos, una gran cantidad de relaciones, que sólo pueden hacerse visibles a través de una lectura adecuada de los mismos. Por esto mismo, la enseñanza de la Matemática tiene dos frentes fundamentales: la conexión directa con el medio, para la observación y conceptualización de lo observado, el establecimiento de una línea de razonamiento, y la aplicación de los parámetros de traducción.
 Esto aplica también en los procesos de solución de problemas, ya que no hay distinción entre los problemas matemáticos y los problemas no matemáticos, porque a fín de cuentas son problemas. La estrategia creada por el matemático húngaro George Pólya para la solución de problemas, si bien se ve, no muestra elemento alguno que no sea de aplicación general en todo contexto. La diferencia radica en el tipo de código que empleamos para la expresión de ese problema (según la información disponible) y, por consiguiente, para su solución y revisión.
Esto aplica también en los procesos de solución de problemas, ya que no hay distinción entre los problemas matemáticos y los problemas no matemáticos, porque a fín de cuentas son problemas. La estrategia creada por el matemático húngaro George Pólya para la solución de problemas, si bien se ve, no muestra elemento alguno que no sea de aplicación general en todo contexto. La diferencia radica en el tipo de código que empleamos para la expresión de ese problema (según la información disponible) y, por consiguiente, para su solución y revisión.Considerando entonces que el pensamiento matemático es el pensamiento para explicar lo que observamos, y que el lenguaje matemático se comporta exactamente como nuestra lengua, pero empleando otros sistemas simbólicos, es posible decir dos cosas:
- El lenguaje matemático puede ser empleado para la representación de cualquier contexto relacionado con la observación de fenómenos. Esto es sabido por la mayoría de las personas, pero aparentemente, no es lo suficientemente claro.
- Como lenguaje, es susceptible de estudio desde los fundamentos teóricos asociados a la adquisición, enseñanza y aprendizaje del lenguaje. No son desatinados los estudios que muestran la conexión especial que hay entre la Matemática y la Lingüística; la Dra. Marta Macho Stadler, de la Universidad del País Vasco, es una de las investigadoras hispanohablantes más conocidas en este tema.
Algo al respecto escribimos mi compañero Sergio Gallo y yo, tratando de mostrar que, a partir de la concepción de la Matemática y la Música como lenguajes, es posible establecer una relación entre estos saberes y los métodos creados para la enseñanza de una segunda lengua. El texto está disponible en mi entrada de LinkedIn Pulse, Possibilities of Linguistic Teaching Methods on Musical and Mathematical Languages Learning: reflections about our practice.
En suma, el razonamiento matemático es el razonamiento en sí, pero empleando como forma de expresión un lenguaje rico en símbolos que dan forma a objetos, situaciones, momentos, fenómenos naturales, ¡incluso adivinanzas! (¿o acaso qué crees que significa "encriptar"?). No por nada se considera a la Matemática el Lenguaje Universal. Viéndolo así, ¿será que en la famosa Torre de Babel se hablaba en Matemático?
Hasta luego.

No hay comentarios:
Publicar un comentario